概率优势与随机幸运
你的策略真的有盈利的能力吗?还是说只是一次随机幸运的结果?不管你是量化交易者还是主观交易者,如果在这个问题上你没有想清楚,那么你开发再多的策略,复盘再多的时间,都是毫无意义的。
什么是真正的交易优势?
首先让我们用聪明的大脑来思考一下什么是真正的交易优势。这里我分享一下个人观点:优势是指我们所采用的交易策略与其他市场交易者的平均水平相比,是否具备更高的成功概率或更大的盈亏比。换句话说,如果我们投入同样的成本,能否获取超过市场平均水平的回报?如果答案是肯定的,那么这个策略就具备了概率优势。
模拟实验:随机策略的假象
我们通过Python代码模拟一个交易策略:
- 胜率49%
- 盈亏比1:1
- 交易笔数500次
- 初始资金1000
这是一个明显无盈利优势的策略(考虑交易成本后必然亏损)。但当我们执行该策略时,资金曲线有时显示盈利(>1000),有时亏损(<1000)。更关键的是,当我们模拟50个同类垃圾策略时,总会有个别策略的资金曲线看似表现良好。这种现象揭示了金融市场的残酷现实:随机性会导致短期假性优势。
python
from matplotlib import pyplot as plt
def simulate_traders(num_trades, balance, win_chance, loss_chance, return_ratio, loss_ratio):
import random
equity_curve = [balance]
current_balance = balance
for _ in range(num_trades):
if random.random() < win_chance:
current_balance *= (1 + return_ratio)
else:
current_balance *= (1 - loss_ratio)
equity_curve.append(current_balance)
return equity_curve
num_curves = 50
num_trades = 500
initial_balance = 1000
random_win_chance = 0.49
random_return_ratio = 0.01
random_loss_ratio = 0.01
random_loss_chance = 1 - random_win_chance
random_curves = []
for _ in range(num_curves):
random_curve = simulate_traders(
num_trades=num_trades,
balance=initial_balance,
win_chance=random_win_chance,
loss_chance=random_loss_chance,
return_ratio=random_return_ratio,
loss_ratio=random_loss_ratio
)
random_curves.append(random_curve)
# 画出所有的随机策略的资金曲线
for i in range(num_curves):
plt.plot(range(num_trades+1), random_curves[i])
plt.title("Equity Curve")
plt.legend(labels=[""])
plt.grid(True)
plt.show()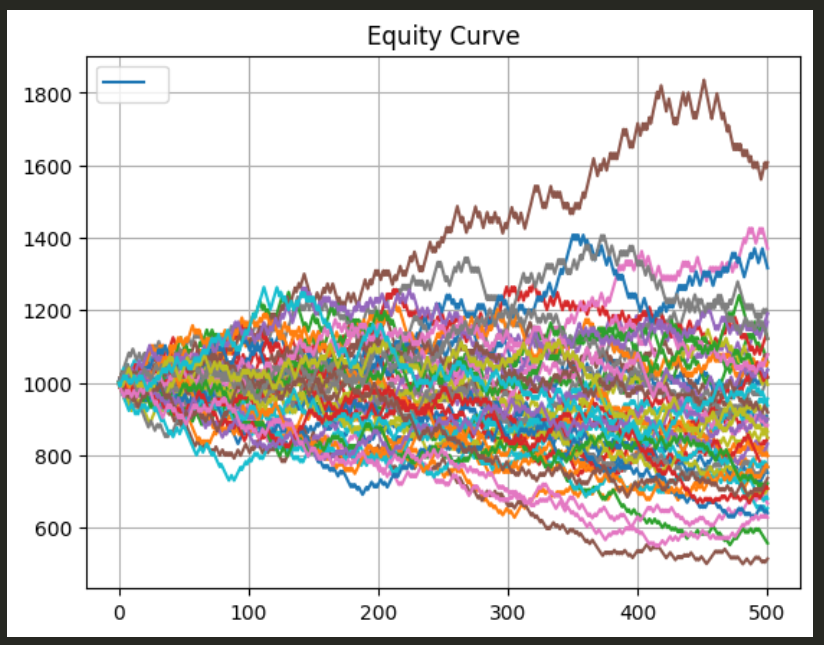
概率优势的验证
我们引入一个真正具备概率优势的策略用红色标注出来:
- 胜率提升至54%
- 保持1:1盈亏比
python
def plot_equty_curves(num_curves, num_trades, random_params, advantage_params, advantage_color):
# 生成随机策略的曲线(多条)
random_curves = []
for _ in range(num_curves):
curve = simulate_traders(
num_trades=num_trades,
balance=random_params[0],
win_chance=random_params[1],
loss_chance=random_params[2],
return_ratio=random_params[3],
loss_ratio=random_params[4]
)
random_curves.append(curve)
# 生成优势策略的曲线(只1条)
advantage_curve = simulate_traders(
num_trades=num_trades,
balance=advantage_params[0],
win_chance=advantage_params[1],
loss_chance=advantage_params[2],
return_ratio=advantage_params[3],
loss_ratio=advantage_params[4]
)
# 创建画布
plt.figure(figsize=(12, 6))
# 绘制随机策略的曲线(蓝色半透明)
for curve in random_curves:
plt.plot(range(num_trades+1), curve, color='blue', alpha=0.3, linewidth=1)
# 绘制优势策略的曲线(单独1条,红色加粗)
plt.plot(range(num_trades+1), advantage_curve, color=advantage_color, linewidth=2, label='Advantage Strategy')
# 添加标签和样式
plt.title("Random Strategies vs. Advantage Strategy", fontsize=14)
plt.xlabel("Number of Trades", fontsize=12)
plt.ylabel("Balance", fontsize=12)
plt.grid(True, alpha=0.5)
plt.legend() # 显示优势曲线的图例
plt.show()
random_parameters = [initial_balance,0.49,1-0.49,0.01,0.01]
advantage_parameters = [initial_balance,0.54,1-0.54,0.01,0.01]
plot_equty_curves(50,500,random_parameters,advantage_parameters,"red")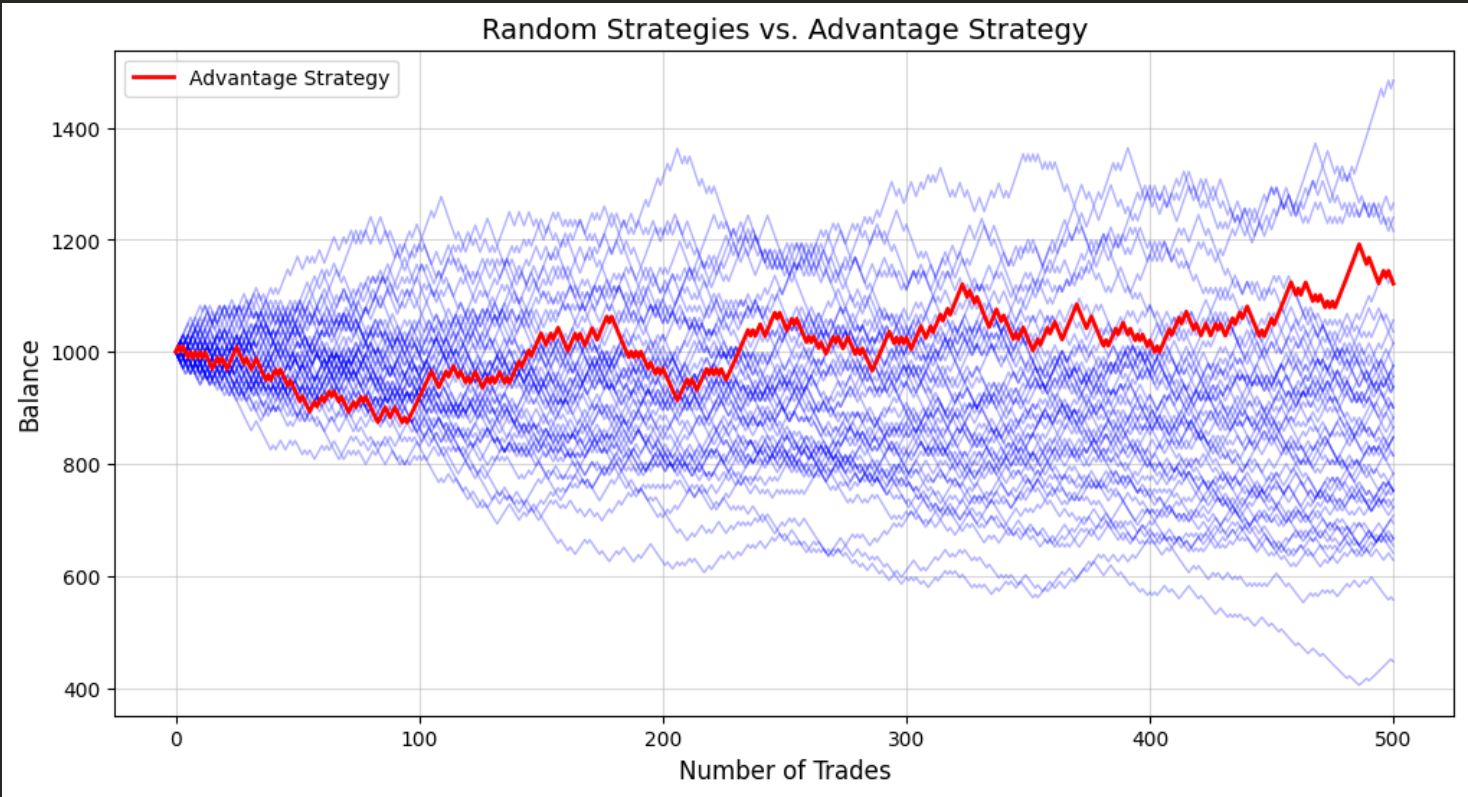
- 交易笔数增加至3000次
python
random_parameters = [initial_balance,0.49,1-0.49,0.01,0.01]
advantage_parameters = [initial_balance,0.54,1-0.54,0.01,0.01]
plot_equty_curves(50,3000,random_parameters,advantage_parameters,"red")将其实测结果(红色曲线)与50个随机策略对比:
- 短期表现(500次交易):优势策略可能落后于随机策略
- 长期表现(3000次交易):优势策略显著跑赢随机策略
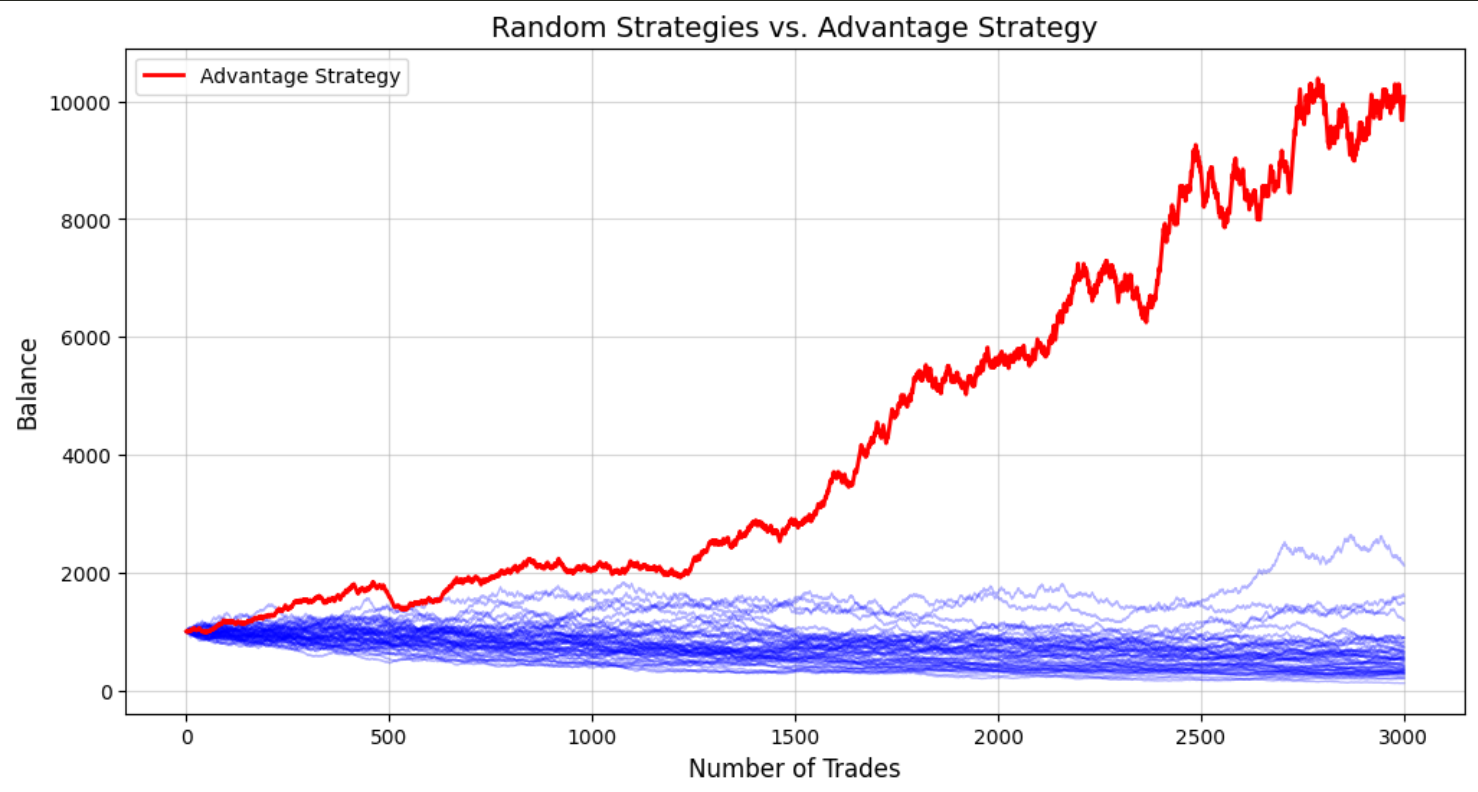
关键结论
1. 样本数量的决定性作用
- 小样本回测(100-500笔交易):结果具有强随机性,无法验证策略有效性
- 大样本验证(3000+笔交易):才能体现真实的概率优势
2. 人性与现实的冲突
- 短期期望管理:即使优势策略也可能需要忍受阶段性亏损,很多人都等不到胜利的果实就已经放弃了
- 大数定律实践:只有足够多的交易次数才能让样本均值趋近理论期望值
给开发者的建议
- 警惕完美回测曲线:需区分概率优势与随机幸运
- 建立科学验证流程:
- 多周期测试
- 蒙特卡洛模拟
- 交易成本精确计算
- 实盘心理建设:接受短期结果与长期预期的背离
"市场上最危险的幻觉,就是把运气当作能力。" —— 无名交易员